Unidad II. Límites y continuidad.

Objetivo II

El alumno comprenderá la noción de límite y de continuidad de una función; las propiedades de los límites y los casos especiales de los límites. Aprenderá a calcular el límite de una función.

 2.1 Definición de límite.

 En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. El límite de una función es un concepto fundamental del cálculo diferencial matemático.

Informalmente, el hecho que una función f tiene un límite L en el punto p, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a p, pero distintos de p.
En análisis real para funciones de una variable, se puede hacer una definición de límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. Esto se puede generalizar aún más a funciones de varias variables o funciones en distintos espacios métricos.

Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:

si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.

Para un mayor rigor matemático se utiliza la definición épsilon-delta de límite, que es más estricta y convierte al límite en una gran herramienta del análisis real. Su definición es la siguiente:

"El límite de f(x) cuando x tiende a c es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δmayor que cero tal que si la distancia entre x y c es menor que δ, entonces la distancia entre la imagen de x y L es menor que εunidades".

Esta definición, se puede escribir utilizando términos lógico-matemáticos y de manera compacta:

Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguientes propiedades o reglas: 

 http://giupidapa.blogspot.mx/2012/10/en-matematica-el-limite-un-concepto-que.html

2.2 Propiedades de los límites.

Límite de una constante

Límite de una suma

Límite de un producto

Límite de un cociente

Límite de una potencia

Límite de una función

g puede ser una raíz, un log, sen ,cos, tg, etc.

Límite de una raíz

Límite de un logaritmo

 

http://www.vitutor.com/fun/3/a_5.html

2.3 Límites laterales.

El límte lateral por la derecha de una función y = f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores mayores que a . 

El límite lateral por la izquierda de una función y=f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores menores que a . 

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera

• x ® a^- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.

• x ® a⁺ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.

Límite lateral por izquierda   si dado e > 0, $ d > 0 tal que si a - d < x < a Þ

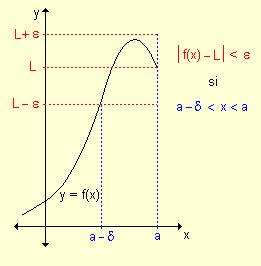Límite lateral por derecha   si dado e > 0, $ d > 0 tal que si a < x < a + d Þ

 Observación. Una función tiene límite si los límites laterales son iguales, es decir, cuando L- =L+
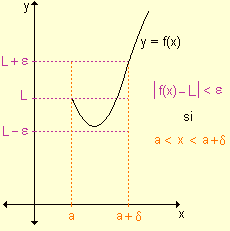http://www.vitutor.com/fun/3/a_2.html

2.4 Límites al infinito.

Sea f una función definida en cada número de algún intervalo I que contiene a, a, excepto posiblemente en a misma. Conforme x se aproxima a a,   crece sin límite lo cual se escribe como

Límite infinito

Una función f(x) tiene por límite +∞ cuando x a, si fijado un número real positivo K>0 se verifica que f(x)>k para todos los valores próximos a a.

Límite menos infinito

Una función f(x) tiene por límite -∞ cuando x a, si fijado un número real negativo K < 0 se verifica que f(x) < k para todos los valores próximos a a.



 https://alexisobed.wordpress.com/3-6-limites-infinitos-y-limites-al-infinito/

2.5 Continuidad y discontinuidad.

En esencia, una función es continua si su gráfica es una línea seguida, no interrumpida.

La definición matemática de continuidad comprende las propiedades de los límites. En la definición de límite el valor de no se especifica; es decir este límite depende únicamente de los valores de en la vecindad de (o sea, cerca de), pero no en el valor de .

Por consiguiente, puede ser o no ser igual a.

Si existe, y también existe el valor de, siendo igual a, entonces es continua en.

Es decir, se dice que una función es continua en si:

Entonces se puede decir que una función f (X) es continua en (o sobre) un intervalo (o bien) si es continua en cada punto del intervalo en cuestión.

De la definición de continuidad se deduce que la gráfica de una función que es continua en un intervalo, es una línea ininterrumpida (es decir, una que se puede trazar sin levantar la pluma o lápiz del papel) sobre el espacio de ese intervalo, o también se hace posible trazar una curva con sólo situar unos pocos puntos y dibujar una línea con trazo ininterrumpido pasando por ellos, se justificará en el caso de varias clases de curvas.

 Discontinuidad.

Con respecto a lo anterior podemos decir que una función es discontinua cuando, una función f definida en un intervalo abierto que contenga a ɑ es discontinua en ɑ si:

f no tiene limite cuando x —> ɑ

cuando x —> ɑ, f tiene un límite diferente de f(ɑ)

si f no está definida en ɑ, no es continua allí. Sin embargo, si f no está definida en ɑ pero si está definida para todos los valores cercanos, entonces no solo no es continua en ɑ, es discontinua allí.

En la figura 9.27 podemos encontrar por inspección puntos de discontinuidad.

http://html.rincondelvago.com/funciones-continuas-y-discontinuas_1.html 

2.6 Aplicaciones a las ciencias económico administrativas; interés compuesto continuamente, límite de la función costo promedio.

Para el interés compuesto, calculamos el interés del primer periodo, lo sumamos al total, y después calculamos el interés del siguiente periodo, y sigue... así: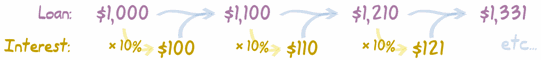

Aquí tienes los cálculos para un préstamo de 5 años al 10%:

Año	Préstamo inicial	Interés	Préstamo final
0 (Ahora)	$1,000.00	($1,000.00 × 10% = ) $100.00	$1,100.00
1	$1,100.00	($1,100.00 × 10% = ) $110.00	$1,210.00
2	$1,210.00	($1,210.00 × 10% = ) $121.00	$1,331.00
3	$1,331.00	($1,331.00 × 10% = ) $133.10	$1,464.10
4	$1,464.10	($1,464.10 × 10% = ) $146.41	$1,610.51
5	$1,610.51

Como ves, es fácil calcular si vas paso a paso.

1. Calcula el interés (= "préstamo inicial" × tasa de interés)
2. Suma el interés al "préstamo inicial" para calcular el "préstamo final" del año
3. El "préstamo final" del año es el "préstamo inicial" del año siguiente

http://www.disfrutalasmatematicas.com/dinero/interes-compuesto.html

 En esta segunda unidad vimos que eran los límites así como sus propiedades.
Que existen varios tipos de límites como los laterales que toman valores del lado izquierdo como derecho de un determinado punto. Los que son al infinito que puede ser cualquier numero y puede ser tanto positivo como negativo.
Al momento de graficar una función dependiendo su límite vamos a ver si es continua o discontinua, si esta va tener un punto de corte o si va  toda recta.