OBJETIVO GENERAL
El estudiante adquirirá destreza en el manejo de técnicas y procedimientos para la solución de problemas. Hará uso de lenguaje matemático, de las sistematización de información y de las formas de representación gráfica y analítica. Manejará los conocimientos, métodos y algoritmos matemáticos establecidos en los programas, tanto básicos como auxiliares para abordar los contenidos de otras materias. Elaborará y usará modelos matemáticos en la resolución de problemas de optimización de recursos.Unidad I. Funciones.
OBJETIVO I1. El alumno entenderá el concepto de función y su manipulación algebraica, así como su representación gráfica. Resolverá problemas de aplicación dando especial énfasis a aquellos relacionados con las áreas económico administrativas, tales como la Economia, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.
1.1 Definición y notación de una función.
En matemáticas, una función, aplicación f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por:Comúnmente, el término función se utiliza cuando el codominio son valores numéricos, reales o complejos. Entonces se habla de función real o función compleja mientras que a las funciones entre conjuntos cualesquiera se las denomina aplicaciones.
En muchos campos aplicados, inclusive a veces en textos de matemáticas, se encuentra la expresión "la función f(x)". De acuerdo a nuestra definición actual, lo anterior no hace sentido, ya que f(x) es una notación para el elemento del codominio. Otras veces, nos encontramos con algo así como "la función f(x) = x^2 - 3x + 7". Aunque aquí hay una posible asignación, no se ha especificado ni el dominio ni el codominio, por lo que en rigor la función f no está bien definida. En ciertos contextos, por ejemplo de funciones numéricas (dominio y codominio son subconjuntos de los Reales.
Las funciones se pueden representar graficamente en el plano cartesiano a través de un graficador el cual se constituye en una herramienta muy poderosa para simplificar los procesos.
Pulse aquí para descargar un programa que nos permite hacer gráficas.
http://funcionesespecializacion.blogspot.mx/2010/10/la-notacion-funcional.html
1.2 Dominio y Rango de una Función.
Como los valores de la función están dados para la variable independiente (x), los valores que puede tomar la función son aquellos para los cuales al evaluar la función para un valor de x, su resultado nos da un número Real. Por ejemplo la función:
f(x) =
Para buscar el dominio de la función, se debe analizar para qué valores de x la función produce como resultado un número Real. Se observa, para el ejemplo que al asignarle a x un número negativo, la expresión se nos presenta como una raíz cuadrada de un número negativo, lo cual no es posible; no es posible hallar dentro de los Reales un número que satisfaga la expresión; por lo tanto el dominio de la función está constituido por todos los números mayores o iguales que cero; expresado como:
En general se pueden seguir las siguientes recomendaciones para obtener el dominio de una función o de una expresión algebraica:
- No puede haber una raíz cuadrada ( ó cualquier raíz par ) negativa, pues se trataría de un número imaginario que no hace parte de los Reales.
- Un fraccionario no puede contener por denominador cero, pues la expresión queda indeterminada.
Por ejemplo:
Si x=2, evaluamos f(2) = 2 ^2 = 4. Y así podemos hacerlo con cualquier número, positivo o negativo. Como x está elevada al cuadrado todos los valores resultantes (es decir de salida) son positivos. Con lo anterior se obtiene que el rango está conformado por el cero y todos los números positivos.
Al graficar la función se obtiene:

Para obtener el rango desde el punto de vista gráfico, debemos poner nuestra atención en el eje y. Se puede ver que el rango está dado por valores mayores o iguales que cero, pues la parábola que lo representa esta ubicada del eje x hacia arriba. Con esto, y lo explicado anteriormente el rango es:
Las funciones tienen gran cantidad de aplicaciones, en la ingeniería por ejemplo cuando la resistencia de un material está en función de las horas de trabajo, en la desintegración radiactiva cuando esta depende del tiempo transcurrido, así como las tasas de crecimiento poblacional, en los cálculos de tasas de interés, etc.
http://artigoo.com/dominio-y-rango-de-una-funcion
1.3 Tipos de funciones.
Funciones algebraicas
En las funciones algebraicas las operaciones que hay
que efectuar con la variable independiente son: la adición, sustracción,
multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas
Si se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x − 2
Funciones implícitas
Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x − y − 2 = 0
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn
Su dominio es  , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.
 , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.Funciones constantes
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones polinómica de primer grado
f(x) = mx + n
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
Son funciones de este tipo las siguientes:
Funciones cuadráticas
f(x) = ax² + bx + c
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
Funciones racionales
El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
Funciones radicales
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par
está formado por todos los valores que hacen que el radicando sea mayor o
igual que cero.
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Funciones trascendentes
La variable independiente figura como exponente, o
como índice de la raíz, o se halla afectada del signo logaritmo o de
cualquiera de los signos que emplea la trigonometría.
Funciones exponenciales

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
Funciones logarítmicas
La función logarítmica en base a es la función inversa de la exponencial en base a.


Funciones trigonométricas
Función seno
f(x) = sen x
Función coseno
f(x) = cos x
Función tangente
f(x) = tg x
Función cosecante
f(x) = cosec x
Función secante
f(x) = sec x
Función cotangente
f(x) = cotg x
1.4 Operaciones con funciones.
Suma de
funciones
Sean f y
g dos funciones reales de
variable real definidas en un mismo intervalo. Se llama suma de ambas
funciones, y se representa por f + g, a la función
definida por
Resta de
funciones
Del mismo modo que se ha definido la suma de funciones, se define
la resta de dos funciones reales de variable real f y g, como la función
Para que esto sea posible es necesario que f y g estén definidas en
un mismo intervalo.
Producto de
funciones
Sean f y g
dos funciones reales de variable real, y definidas en un mismo
intervalo. Se llama función producto de f
y g a la función definida por
Cociente de
funciones
Dadas dos funciones reales de variable real, f y g, y definidas en un
mismo intervalo, se llama función cociente de f
y g a la función definida por
(La función f/g está
definida en todos los puntos en los que la función g no se anula.)
Producto de
un número por una función
Dado un número real a y
una función f, el producto
del número por la función es la función definida por
1.5 Composición de Funciones.
Dadas dos funciones reales de variable real, f y g, se llama composición
de las
funciones f y g, y se escribe
g o f, a la función
definida de R en R, por (g o f )(x) = g[f(x)].
La función ( g o f )(x) se lee « f
compuesto con g aplicado a x ».
Primero actúa la función f
y después actúa la función g,
sobre f(x).
Cálculo de
la imagen de un elemento mediante una función compuesta
Para obtener la imagen de la función compuesta aplicada a un número
x, se siguen estos pasos:
1. Se calcula la imagen de x
mediante la función f, f(x).
2. Se calcula la imagen mediante la función g, de f(x).
Es decir, se aplica la función g
al resultado obtenido anteriormente.
Ejercicio:
Sean las
funciones f(x)
= x + 3 y g(x) = x2.
Calcular g o f y la imagen mediante esta función de 1, 0 y -3.
Resolución:
· La imagen de dos
números 1, 0, -3, mediante la función g
o
f es:
‚ Dadas las
funciones f(x)
= x2
+ 1, y g(x) = 3x - 2, calcular:
a) (g o
f ) (x)
b) (f o
g ) (x)
c) (g o
f ) (1) y (f o g ) (-1)
d ) El original de
49 para la función g o f.
Resolución:
c) Aplicando los resultados de los apartados anteriores:
(g o
f ) (x)
= 3x2
+ 1 = 49. Basta con resolver esta ecuación.
1.6 Gráfica de una función.
La gráfica de una función está formada por el conjunto de puntos (x, y) cuando x varía en el dominio D.
gráfica (f) = {(x, f(x)) /  x ∈ D}
x ∈ D}
 x ∈ D}
x ∈ D}
Para representarla
calcularemos aquellos puntos o intervalos donde la función tiene un
comportamiento especial, que determinaremos mediante el estudio de los
siguientes apartados:
1. Dominio de la función.
2. Simetría
3. Periodicidad
4. Puntos de corte con los ejes.
5. Asíntotas
6. Ramas parabólicas
7. Crecimiento y Decrecimiento
8. Máximos y mínimos
9. Concavidad y convexidad
10. Puntos de inflexión
Ejemplo de representación de una función

Dominio

Simetría

Simetría respecto al origen, es decir, la función es impar
Puntos de corte
Punto de corte con OX:

Punto de corte con OY:

Asíntotas
Asíntota horizontal

No tiene asíntotas verticales ni oblicuas
Crecimiento y de crecimiento




Máximos y mínimos
Candidatos a extremos: x = − 1 y x = 1.





Concavidad y convexidad




Puntos de inflexión

Representación gráfica
http://www.vitutor.com/fun/5/c_1.html

1.7 Función lineal y función cuadrática.
Función Lineal
La función lineal es del tipo:
y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.
y = 2x| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y = 2x | 0 | 2 | 4 | 6 | 8 |

Pendiente
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.

Función Cuadrática
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
f(x) = ax² + bx + c
Representación gráfica de la parábola
Podemos construir una parábola a partir de estos puntos:
1. Vértice

Por el vértice pasa el eje de simetría de la parábola.
La ecuación del eje de simetría es:

2. Puntos de corte con el eje OX
En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:
ax² + bx + c = 0
Resolviendo la ecuación podemos obtener:
Dos puntos de corte: (x1, 0) y (x2, 0) si b² − 4ac > 0
Un punto de corte: (x1, 0) si b² − 4ac = 0
Ningún punto de corte si b² − 4ac < 0
3. Punto de corte con el eje OY
En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:
f(0) = a · 0² + b · 0 + c = c (0,c)
Ejemplo
Representar la función f(x) = x² − 4x + 3.
1. Vértice
xv = − (−4) / 2 = 2 yv= 2² − 4· 2 + 3 = −1
V(2, −1)
2. Puntos de corte con el eje OX
x² − 4x + 3 = 0

(3, 0) (1, 0)
3. Punto de corte con el eje OY
(0, 3)

1.8 Función exponencial y logarítmica.
Función Exponencial.
Definición: Una función exponencial con base b es
una función de la forma f(x) = bx ,
donde b y x son números reales tal que b >
0 y
b es diferente de uno.
El
dominio es el conjunto de todos los números reales y el recorrido es el conjunto de todos los
números reales positivos.
1)
f(x) = 2x


Propiedades
de f(x) = bx, b>0, b diferente de uno:
1) Todas las gráficas intersecan en el punto
(0,1).
2) Todas las gráficas son continuas, sin huecos
o saltos.
3) El eje de x es la asíntota horizontal.
4) Si b
> 1 (b, base), entonces bx aumenta conforme aumenta x.
5) Si 0
< b < 1, entonces bx disminuye conforme aumenta x.
6) La función f es una función uno a uno.
Propiedades
de las funciones exponenciales: Para a y b positivos, donde a y b son diferentes de
uno y x, y reales:
1)
Leyes de los exponentes:

2) ax = ay si y sólo si x = y
3) Para x diferente de cero, entonces ax
= bx si y sólo si a = b.
Las funciones lineales y cuadráticas
se pueden escribir de la forma f(x) = mx + b, y f(x) = ax2 + bx + c
respectivamente, quieres saber a detalle que son las funciones lineales y
cuadráticas, cómo se representan en la gráfica y algunos ejemplos? Sigue leyendo!

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.
Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.

a, b y c = números reales diferentes a cero.
Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.
La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.
Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.
Para obtener la raíces de la ecuación seguimos estos pasos:
- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.masELTa0.dpuf
Una función logarítmica es aquella que genéricamente se expresa como f (x) == logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1. Funciones lineales y cuadráticas
Funciones lineales

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
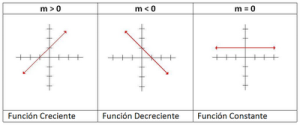
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
Estos son los tres tipos de funciones:
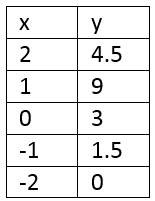
Ejemplo
Tenemos la siguiente función: y = 1.5 x + 3la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.
Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.

Funciones cuadráticas
Una función cuadrática es una función polinómica de segundo grado que se escribe : f(x) = ax2 + bx + c
a, b y c = números reales diferentes a cero.
Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.
La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.
Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.
Para obtener la raíces de la ecuación seguimos estos pasos:
- Igualar la ecuación a cero.
- Factorizar la ecuación.
- Igualar cada factor a cero y obtener las raíces.
- Con el valor de “a” determinar si la parábola abre hacía arriba o hacía abajo.
- Obtener los puntos de intersección, los del eje “x” se obtienen con las raíces de la ecuación, para obtener las intersecciones en “y” igualamos la x a cero.
- Obtener el vértice de la función, el punto “x” de la coordenada del vértice se obtiene con la fórmula -b/2a y el punto “y” se obtiene sustituyendo x en la función.
- Graficar los puntos obtenidos en los puntos 2 y 3 para graficar la curva.
- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.masELTa0.dpuf
La función logarítmica es la inversa de la función exponencial (ver t35), dado que:
loga x = b Û ab = x.
 Representación gráfica de funciones logarítmicas y de sus inversas (exponenciales).
Representación gráfica de funciones logarítmicas y de sus inversas (exponenciales).
Las funciones lineales y cuadráticas
se pueden escribir de la forma f(x) = mx + b, y f(x) = ax2 + bx + c
respectivamente, quieres saber a detalle que son las funciones lineales y
cuadráticas, cómo se representan en la gráfica y algunos ejemplos? Sigue leyendo!

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.
Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.


a, b y c = números reales diferentes a cero.
Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.
La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.
Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.
Para obtener la raíces de la ecuación seguimos estos pasos:
- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.masELTa0.dpuf
Funciones lineales y cuadráticas
Funciones lineales

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
Estos son los tres tipos de funciones:
Ejemplo
Tenemos la siguiente función: y = 1.5 x + 3la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.
Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.

Funciones cuadráticas
Una función cuadrática es una función polinómica de segundo grado que se escribe : f(x) = ax2 + bx + c
a, b y c = números reales diferentes a cero.
Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.
La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.
Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.
Para obtener la raíces de la ecuación seguimos estos pasos:
- Igualar la ecuación a cero.
- Factorizar la ecuación.
- Igualar cada factor a cero y obtener las raíces.
- Con el valor de “a” determinar si la parábola abre hacía arriba o hacía abajo.
- Obtener los puntos de intersección, los del eje “x” se obtienen con las raíces de la ecuación, para obtener las intersecciones en “y” igualamos la x a cero.
- Obtener el vértice de la función, el punto “x” de la coordenada del vértice se obtiene con la fórmula -b/2a y el punto “y” se obtiene sustituyendo x en la función.
- Graficar los puntos obtenidos en los puntos 2 y 3 para graficar la curva.
- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.masELTa0.dpuf
1.9 Aplicaciones en las ciencias económico administrativas: funciones de oferta y demanda; recta presupuestal, funciones de ingresos, costos y utilidades; funciones de apreciación y depreciación.
Las ecuaciones de oferta y demanda.
Para establecer
el punto de equilibrio es necesario determinar las ecuaciones de oferta
y demanda, las cuales tienen la siguiente forma:
De
donde:
p: es el precio del producto
q: la cantidad de unidades a ofrecer o demandar,
según sea el caso (oferta o demanda)
m:
la pendiente es una constante positiva en el caso de la oferta y negativa
para el caso de la demanda
Para determinar
la ecuación de oferta se
tienen los siguientes datos:
Si el precio
se fija en $220.00 entonces la oferta es de 20,000 unidades, es decir:
si
q =
20000 entonces p = 220.00
Si el precio
se fija en $227.00 entonces la oferta es de 27,000 unidades, es decir:
si
q =
27000 entonces p = 227.00
http://www.eva.com.mx/sia/facs/Talleres/mate1/avanzau4r4.htm
En esta primer unidad comenzamos a ver sobre las funciones desde su significado hasta la notación que se utiliza, en este tipo de funciones se maneja que tienen un dominio y un rango que puede ser cualquier numero real.
Hay distintos tipos de funciones como lo son las algebraicas que se dividen en polinomicas, racionales, radicales y a trozos; y las trascendentes que se dividen en exponenciales, logaritmicas y trigonométricas.
Estuvimos viendo la definición de cada una de estas y sus propiedades, para poder comprender realizamos algunos ejercicios.
Para saber como se hacian ejercicios de funciones con operaciones normales y después poder graficarlas.
En esta primer unidad comenzamos a ver sobre las funciones desde su significado hasta la notación que se utiliza, en este tipo de funciones se maneja que tienen un dominio y un rango que puede ser cualquier numero real.
Hay distintos tipos de funciones como lo son las algebraicas que se dividen en polinomicas, racionales, radicales y a trozos; y las trascendentes que se dividen en exponenciales, logaritmicas y trigonométricas.
Estuvimos viendo la definición de cada una de estas y sus propiedades, para poder comprender realizamos algunos ejercicios.
Para saber como se hacian ejercicios de funciones con operaciones normales y después poder graficarlas.
Las funciones lineales y cuadráticas
se pueden escribir de la forma f(x) = mx + b, y f(x) = ax2 + bx + c
respectivamente, quieres saber a detalle que son las funciones lineales y
cuadráticas, cómo se representan en la gráfica y algunos ejemplos? Sigue leyendo!

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.
Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.


a, b y c = números reales diferentes a cero.
Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.
La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.
Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.
Para obtener la raíces de la ecuación seguimos estos pasos:
- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.masELTa0.dpuf
Funciones lineales y cuadráticas
Funciones lineales

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
Estos son los tres tipos de funciones:
Ejemplo
Tenemos la siguiente función: y = 1.5 x + 3la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.
Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.

Funciones cuadráticas
Una función cuadrática es una función polinómica de segundo grado que se escribe : f(x) = ax2 + bx + c
a, b y c = números reales diferentes a cero.
Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.
La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.
Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.
Para obtener la raíces de la ecuación seguimos estos pasos:
- Igualar la ecuación a cero.
- Factorizar la ecuación.
- Igualar cada factor a cero y obtener las raíces.
- Con el valor de “a” determinar si la parábola abre hacía arriba o hacía abajo.
- Obtener los puntos de intersección, los del eje “x” se obtienen con las raíces de la ecuación, para obtener las intersecciones en “y” igualamos la x a cero.
- Obtener el vértice de la función, el punto “x” de la coordenada del vértice se obtiene con la fórmula -b/2a y el punto “y” se obtiene sustituyendo x en la función.
- Graficar los puntos obtenidos en los puntos 2 y 3 para graficar la curva.
- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.masELTa0.dpuf



Buen trabajo.!
ResponderEliminarMuy buen trabajo!!!!
ResponderEliminarBuen blog andrea
ResponderEliminarmuy buen trabajo
ResponderEliminarMuy bueno andrea
ResponderEliminarMuy bueno andrea
ResponderEliminarmuy buen blog andrea =) saka los takos jejeje
ResponderEliminarbuen trabajo
ResponderEliminarmuy bueno andrea ee ;)
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarandrea :)
ResponderEliminarme encanto Andrea! que buen trabajo
ResponderEliminarmuy buen blog
ResponderEliminar